Las funciones exponenciales son un tema fundamental en matemáticas y se utilizan en diversos campos de la ciencia y la tecnología. En este artículo, exploraremos las características, tipos, aplicaciones y propiedades de las funciones exponenciales. También explicaremos cómo graficar una función exponencial y responderemos algunas preguntas frecuentes.
¿Qué es una función exponencial?
Definición
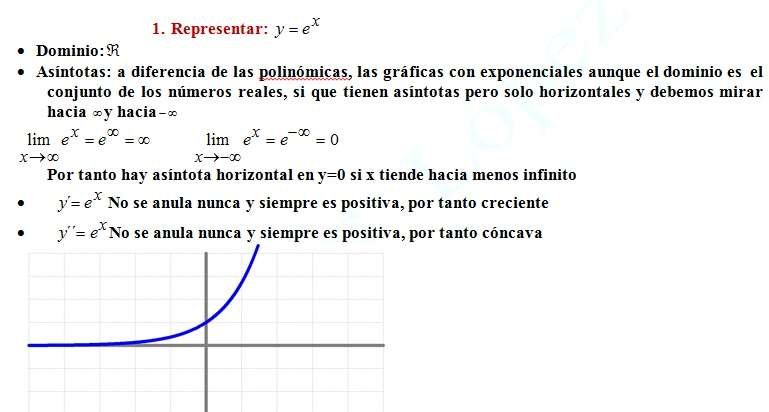
Una función exponencial es una función matemática en la que la variable independiente aparece en el exponente. Su forma general es f(x) = a^x, donde a es la base de la función y x es la variable independiente.
Características
Las funciones exponenciales tienen algunas características importantes, como su comportamiento monótono, su crecimiento o decrecimiento rápido y su tendencia a tener valores cercanos a cero o a infinito. Además, estas funciones pueden ser utilizadas para modelar muchos fenómenos naturales y sociales.
Mira Tambien
Curiosidades de Einstein y la teoría de la relatividadTipos de funciones exponenciales
Función exponencial creciente
Una función exponencial es creciente cuando la base es mayor que 1 y el exponente es positivo. En este caso, la función aumenta rápidamente a medida que x se acerca a infinito y se aproxima a cero a medida que x se acerca a menos infinito.
Función exponencial decreciente
Por otro lado, una función exponencial es decreciente cuando la base es mayor que 1 y el exponente es negativo. En este caso, la función disminuye rápidamente a medida que x se acerca a menos infinito y se aproxima a cero a medida que x se acerca a infinito.
Función exponencial compuesta
También existe una función exponencial compuesta, que es una combinación de una función exponencial y otra función. La forma general de esta función es f(x) = a^g(x), donde g(x) es una función distinta de la constante.
Mira TambienCuriosidades de Einstein y la teoría de la relatividad
Datos curiosos del ácido clorhídrico: composición, usos y propiedadesAplicaciones de las funciones exponenciales
En economía
Las funciones exponenciales se utilizan en economía para modelar el crecimiento exponencial de las inversiones, los precios y los ingresos.
En biología
En biología, las funciones exponenciales se utilizan para modelar el crecimiento exponencial de las poblaciones, el crecimiento de las células y la descomposición de los materiales orgánicos.
En física
En física, las funciones exponenciales se utilizan para modelar el decaimiento radioactivo, el crecimiento de los campos eléctricos y magnéticos y la propagación de ondas.
Mira TambienCuriosidades de Einstein y la teoría de la relatividadDatos curiosos del ácido clorhídrico: composición, usos y propiedades
Curiosidades de los puentes de hidrógenoPropiedades de las funciones exponenciales
Propiedad de monotonía
Las funciones exponenciales son funciones monótonas, lo que significa que siempre aumentan o disminuyen a medida que x se mueve hacia la derecha o hacia la izquierda.
Propiedad de continuidad
Las funciones exponenciales son continuas en todo su dominio, lo que significa que no tienen saltos o huecos en su grafica.
Propiedad de convexidad
Las funciones exponenciales son funciones convexas, lo que significa que su grafica se curva hacia arriba.
Cómo graficar una función exponencial
Paso a paso
Para graficar una función exponencial, sigue estos pasos:
1. Identifica la base a de la función.
2. Encuentra los puntos donde la función cruza el eje y (cuando x es cero).
3. Encuentra los puntos donde la función cruza el eje x (cuando f(x) es cero).
4. Elige algunos valores de x adicionales y encuentra los correspondientes valores de f(x).
5. Grafica los puntos encontrados y dibuja una curva suave que los conecte.
Conclusión
Las funciones exponenciales son una herramienta matemática poderosa que se utiliza en muchos campos de la ciencia y la tecnología. Comprender sus características, tipos, aplicaciones y propiedades puede ayudarnos a entender mejor el mundo que nos rodea.
Preguntas frecuentes
¿Cómo se resuelve una ecuación exponencial?
Para resolver una ecuación exponencial, utiliza propiedades de los logaritmos para despejar la variable exponencial.
¿Cómo se calcula el crecimiento de una función exponencial?
El crecimiento de una función exponencial se puede calcular utilizando la tasa de crecimiento, que es la tasa a la cual la función aumenta o disminuye en un momento dado.
¿Cuáles son las principales aplicaciones de las funciones exponenciales en la vida diaria?
Las principales aplicaciones de las funciones exponenciales en la vida diaria incluyen el crecimiento de la población, los precios de los bienes y servicios, el crecimiento de las inversiones y el decaimiento radioactivo.
¿Qué diferencias hay entre una función exponencial y una función logarítmica?
La principal diferencia entre una función exponencial y una función logarítmica es que la variable independiente aparece en el exponente en una función exponencial y en la base en una función logarítmica. Además, las funciones logarítmicas son la inversa de las funciones exponenciales.
